树状数组总结

字数统计: 2.5k字   |   阅读时长: 13min

写在前面：关于树状数组

首先，要灵活运用树状数组，必须要弄懂lowbit.
lowbit 计算的是一个数二进制的最低位。
lowbit(x)=x&-x;
这是为什么呢???
对于一个正数5，它的二进制为00000000 00000000 00000000 00000101 （longlong范围内）
它的负数的原码为 10000000 00000000 00000000 00000101 （在第64位+1）
（二进制的64位为符号位，0为正数，1为负数）
负数的二进制为它的原码的补码（除符号位按位取反后+1）
也就是11111111 11111111 11111111 11111011
所以x&-x就是x的最低位

插一幅图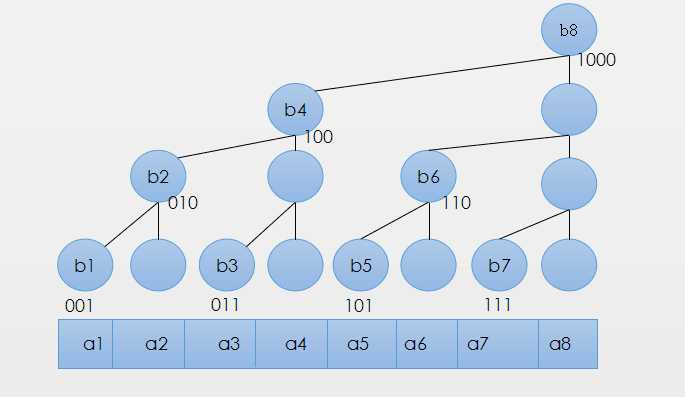

1.lowbit(x)为x的最低位

2.tr[x]存的是x及以前的lowbit(x)-1位的值的和

3.lowbit(x)还可表示tr[x]所维护的区间长度

一. 一维树状数组

1、最简单的单点修改+区间查询

直接上代码。。。

1
2
3
4
5
6
7
8
9
10
11
12
13
inline void add(int x,int v)
{
    for(register int i=x;i<=n;i+=lowbit(i))
    tr[i]+=v;
}

inline int qurey(int x)
{
    int rt=0;
    for(register int i=x;i;i-=lowbit(i))
    rt+=tr[i];
    return rt;
}

2、 稍微难一点点的区间修改+单点查询

这里运用了差分和前缀和的思想。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
inline void add(int x,int v)
{
    for(register int i=x;i<=n;i+=lowbit(i))
    tr[i]+=v;
}

inline int qurey(int x)//单点查询 
{
    int rt=0;
    for(register int i=x;i;i-=lowbit(i))
    rt+=tr[i];
    return rt;
}

inline void change(int l,int r,int v)//区间修改 
{
    add(l,v);add(r+1,-v);
}

3.难一点的区间修改 + 区间查询

(d[i]为差分数组)
我们基于问题2的“差分”思路，考虑一下如何在问题2构建的树状数组中求前缀和：

位置p的前缀和


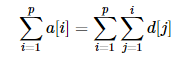
可变为


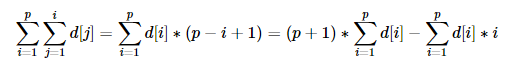
那么我们可以维护两个数组的前缀和：
一个数组是 d1[i](d[i]的前缀和)。
另一个数组是 d2[i](d[i]∗i的前缀和)。

查询

位置p的前缀和即： (p + 1) * d1数组中p的前缀和 - d2数组中p的前缀和。

区间[l, r]的和即：位置r的前缀和 - 位置l-1的前缀和。

修改

对于d1数组的修改同单点修改。

对于d2数组的修改也类似，我们给 d2[l] 加上 l * x，给 d2[r + 1] 减去 (r + 1) * x。

解释：修改操作是由查询操作推得的，对于位置l它需要加上一个x，d1已经加上了一个x，d1*(l+1)后
需要再减去l*x，所以在位置l加上l*x，后面依次类推。

上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

template<class T>
inline void read(T &a)
{
    T f=1;a=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s<='9'&&s>='0'){a=a*10+s-'0';s=getchar();}
    a*=f;
}

ll d1[100100],d2[100100],a[100100];
int n,m;

inline void add(int x,ll v)
{
	for(register int i=x;i<=n;i+=lowbit(i))
    d1[i]+=v,d2[i]+=(ll)v*x;
}

inline void range_add(int l,int r,ll v)
{
    add(l,v),add(r+1,-v);
}

inline ll ask(int p)
{
    ll rt=0;
    for(register int i=p;i;i-=lowbit(i)) 
	rt+=(ll)(p+1)*d1[i]-d2[i];
    return rt;
}

inline ll query(int l,int r)
{
    return ask(r)-ask(l-1);
}

int main()
{
    read(n),read(m);
    for(register int i=1;i<=n;i++) read(a[i]),add(i,a[i]-a[i-1]);
    int opt,x,y;
    ll k;
    while(m--)
    {
        read(opt),read(x),read(y);
        if(opt==1)
        {
            read(k);
            range_add(x,y,k);
        }
        else
        {
            printf("%lld\n",query(x,y));
        }
    }
    return 0;
}

附一模板题:P3372 【模板】线段树 1

4.区间最值

说明:tr[x]表示的是x-lowbit(x)到 x 的区间最值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

template<class T>
inline void read(T &a)
{
	T f=1;a=0;char s=getchar();
	while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
	while(s<='9'&&s>='0'){a=a*10+s-'0';s=getchar();}
	a*=f;
}

int n,m;
ll tr[100100],a[100100]; 

inline void build()
{
	for(register int i=1;i<=n;i++)
	{
		tr[i]=a[i];
		int tmp=(i&-i);
		for(register int j=1;j<tmp;j<<=1) tr[i]=max(tr[i],tr[i-j]);//更新tr[i]的值； 
	}
}

inline void add(int x,ll v)
{
	a[x]=v;
	while(x<=n)
	{
		tr[x]=a[x];
		int tmp=x&-x;
		for(register int j=1;j<tmp;j<<=1) tr[x]=max(tr[x],tr[x-j]);//tr[x]表示的是x-lowbit(x)到 x 的区间最值。 
		x+=(x&-x);
	}
}

inline ll query(int l,int r)
{
	ll ans=a[r];
	while(1)
	{
		ans=max(ans,a[r]);
		if(r==l) break;r--;
		while(r-l>=(r&-r)) ans=max(ans,tr[r]),r-=(r&-r);//(r&-r)为tr[r]维护的区间最值，当 r-l>=(r&-r)时可直接转移。 
	}
	return ans;
}

int main()
{
	read(n),read(m);
	for(register int i=1;i<=n;i++) read(a[i]);
	build();
	int l,r;
	while(m--)
	{
		read(l),read(r);
		printf("%lld\n",query(l,r));
	}
	return 0;
}

二. 二维树状数组

1、单点修改+区间查询

其实多了一维并没有想象中的那么难，我们可以开两颗树状数组，一颗维护一维的值，另一颗维护前一颗树状数组的值。
可以开一个二维数组，tr[x][y]表示从（1,1）到（x，y）的区间和。

不多说上代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include<cstdio>
using namespace std;
typedef long long ll;

template<typename T>
inline void read(T &a)
{
	T f=1;a=0;char s=getchar();
	while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
	while(s<='9'&&s>='0'){a=a*10+s-'0';s=getchar();}
	a*=f;
}

ll tr[1030][1030];

int n;

inline int lowbit(int x){return (x&-x);}

inline void add(int x,int y,ll v)
{
	int tmp=y;
	while(x<=n)
	{
		y=tmp;
		while(y<=n) tr[x][y]+=v,y+=lowbit(y);
		x+=lowbit(x);
	}
}

inline ll range_sum(int x,int y)
{
	ll rt=0;
	int tmp=y;
	while(x)
	{
		y=tmp;
		while(y) rt+=tr[x][y],y-=lowbit(y);
		x-=lowbit(x);
	}
	return rt;
}

inline void query(int x,int y,int x1,int y1)
{
	printf("%lld\n",range_sum(x1,y1)-range_sum(x1,y-1)-range_sum(x-1,y1)+range_sum(x-1,y-1));
}

int main()
{
	int opt,x,y,a,x1,y1;
	while(scanf("%d",&opt))
	{
		if(opt==3) break;
		if(opt==0) read(n);
		if(opt==1) read(x),read(y),read(a),add(++x,++y,a);
		if(opt==2) read(x),read(y),read(x1),read(y1),query(++x,++y,++x1,++y1);
	}
	return 0;
}

题目：POJ 1195

2、区间修改+单点查询

对与区间修改单点查询，我们还沿用一维的套路——差分。

由二维前缀和：sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]可推的。
d[i][j](二维差分数组)=a[i][j]-a[i-1][j]-sum[i][j-1]+a[i-1][j-1]

来一道题目：POJ2155Matrix

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include<cstdio>
#include<cstring>
#include<string>
#define lowbit(x) x&-x
using namespace std;

template<typename T>
inline void read(T &a)
{
	T f=1;a=0;char s=getchar();
	while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
	while(s>='0'&&s<='9'){a=a*10+s-'0';s=getchar();}
	a*=f;
}

int T,n,m;
int tr[1010][1010];

inline void add(int x,int y,int v)
{
	for(register int i=x;i<=n;i+=lowbit(i))
	for(register int j=y;j<=n;j+=lowbit(j))
	tr[i][j]+=v;
}

inline int query(int x,int y)
{
	int rt=0;
	for(register int i=x;i;i-=lowbit(i))
	for(register int j=y;j;j-=lowbit(j))
	rt+=tr[i][j];
	return rt;
}

int main()
{
	read(T);
	char s;
	int x1,y1,x2,y2;
	while(T--)
	{
		read(n),read(m);
		for(register int i=1;i<=m;i++)
		{
			scanf("%c",&s);
			if(s=='C')
			{
				read(x1),read(y1),read(x2),read(y2);
				add(x1,y1,1);
				add(x1,y2+1,-1);
				add(x2+1,y2+1,1);
				add(x2+1,y1,-1);
			}
			else if(s=='Q')
			{
				read(x1),read(y1);
				printf("%d\n",query(x1,y1)&1);
			}
		}
		memset(tr,0,sizeof(tr));
		puts("");
	}
	return 0;
}

3.区间修改+区间查询

(d[i][j]为差分数组)

$$ sum[i][j]=\sum_{x=1}^{i}\sum_{y=1}^{j}\sum_{a=1}^{x}\sum_{b=1}^{y}d[a][b] $$

整理可得：

$$ sum[i][j]=\sum_{x=1}^{i}\sum_{y=1}^{j}d[x][y](i+1-x)(j+1-y) $$

$$ sum[i][j]=(i+1)*(j+1)\sum_{x=1}^{i}\sum_{y=1}^{j}d[x][y]-(i+1)\sum_{x=1}^{i}\sum_{y=1}^{j}d[x][y]*y-(j+1)\sum_{x=1}^{i}\sum_{y=1}^{j}d[x][y]*x+\sum_{x=1}^{i}\sum_{y=1}^{j}d[x][y]xy$$

由上式可的我们须用四个树状数组分别记录d[i][j]*i,d[i][j]*j,d[i][j]ij,和d[i][j]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include<bits/stdc++.h>
#define lowbit(x) x&-x
using namespace std;

template<typename T>
inline void read(T &a)
{
	T f=1;a=0;char s=getchar();
	while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
	while(s<='9'&&s>='0'){a=a*10+s-'0';s=getchar();}
	a*=f;
}

int n,m;
int d1[1010][1010],d2[1010][1010],d3[1000][1010],d4[1010][1010];

inline void add(int x,int y,int v)
{
	for(register int i=x;i<=n;i+=lowbit(i))
	for(register int j=y;j<=m;j+=lowbit(j))
	{
		d1[i][j]+=v;
		d2[i][j]+=y*v;
		d3[i][j]+=x*v;
		d4[i][j]+=x*y*v;
	}
}

inline int query(int x,int y)
{
	int ans=0;
	for(register int i=x;i;i-=lowbit(i))
	for(register int j=y;j;j-=lowbit(j))
	{
		ans+=(x+1)*(y+1)*d1[i][j]-(x+1)*d2[i][j]-(y+1)*d3[i][j]+d4[i][j];
	}
	return ans;
}

inline int matrix_ask(int x,int y,int x1,int y1)
{
	return query(x1,y1)-query(x1,y-1)-query(x-1,y1)+query(x-1,y-1);
}

int main()
{
	char s;
	int a,b,c,d,v;
	scanf("%s",&s);
	if(s=='X') read(n),read(m);
	while(scanf("%s",&s)&&((s=='L')||(s=='k')))
	{
		if(s=='L')
		{
			read(a),read(b),read(c),read(d),read(v);
			add(a,b,v);
			add(c+1,d+1,v);
			add(a,d+1,-v);
			add(c+1,b,-v);
		}
		if(s=='k')
		{
			read(a),read(b),read(c),read(d);
			printf("%d\n",matrix_ask(a,b,c,d));
		}
	}
	return 0;
}
本文作者： syrsteven
最后更新： 2023年09月02日 04:06:21
本文链接： http://syrsteven.github.io/post/30ce1405.html
版权声明： 本作品采用 CC BY-NC-SA 4.0 许可协议进行许可，转载请注明出处！

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

    			  jsonContent:
				meta: false
				pages: false
				posts:
				  title: true
				  date: true
				  path: true
				  text: false
				  raw: false
				  content: false
				  slug: false
				  updated: false
				  comments: false
				  link: false
				  permalink: false
				  excerpt: false
				  categories: false
				  tags: true


There's nothing